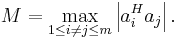Mutual coherence (linear algebra)

In linear algebra, the coherence[1] or mutual coherence[2] of a matrix A is defined as the maximum absolute value of the cross-correlations between the columns of A.

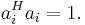Formally, let a_1, \ldots, a_m be the columns of the matrix A, which are assumed to be normalized such that a_i^H a_i = 1. The mutual coherence of A is then defined as[2][1]

M = \max_{1 \le i \ne j \le m} \left| a_i^H a_j \right|.

The concept was introduced in a slightly less general framework by Donoho and Huo,[3] and has since been used extensively in the field of sparse representations of signals. In particular, it is used as a measure of the ability of suboptimal algorithms such as matching pursuit and basis pursuit to correctly identify the true representation of a sparse signal.[4][2][1]

See also

References

  1. ^ a b c Tropp, J.A. (March 2006). "Just relax: Convex programming methods for identifying sparse signals in noise". IEEE Transactions on Information Theory 52 (3): 1030–1051. doi:10.1109/TIT.2005.864420. http://ieeexplore.ieee.org/stamp/stamp.jsp?arnumber=01603770. 
  2. ^ a b c Donoho, D.L.; M. Elad; V.N. Temlyakov (January 2006). "Stable recovery of sparse overcomplete representations in the presence of noise". IEEE Transactions on Information Theory 52 (1): 6–18. doi:10.1109/TIT.2005.860430. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=1564423. 
  3. ^ Donoho, D.L.; Xiaoming Huo (November 2001). "Uncertainty principles and ideal atomic decomposition". IEEE Transactions on Information Theory 47 (7): 2845–2862. doi:10.1109/18.959265. http://ieeexplore.ieee.org/stamp/stamp.jsp?arnumber=00959265. 
  4. ^ Fuchs, J.-J. (June 2004). "On sparse representations in arbitrary redundant bases". IEEE Transactions on Information Theory 50 (6): 1341–1344. doi:10.1109/TIT.2004.828141. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=1302316.